Section 10.2 Second Derivative Test
Why does the second derivative test work?
Recall that first derivatives tell you how to find the linear approximation to a function. For functions of two variables, we have
\begin{equation}
f(x+\Delta x,y+\Delta y) \approx
f(x,y) + \Partial{f}{x}\Delta x + \Partial{f}{y}\Delta y\tag{10.2.1}
\end{equation}
which we can also write as
\begin{equation}
\Delta f \approx \Partial{f}{x}\Delta x + \Partial{f}{y}\Delta y .\tag{10.2.2}
\end{equation}
At a local max/min, however, both partial derivatives vanish, and the linear approximation isn’t good enough to see what is happening. Instead, we need the quadratic approximation, which turns out to be
\begin{equation}
\Delta f \approx \Partial{f}{x}\Delta x + \Partial{f}{y}\Delta y
+ \frac{\partial^2f}{\partial x^2}(\Delta x)^2
+ 2\frac{\partial^2f}{\partial x\partial y}\Delta x\,\Delta y
+ \frac{\partial^2f}{\partial y^2}(\Delta y)^2 .\tag{10.2.3}
\end{equation}
At a local extremum, the first two terms vanish, and we are left with
\begin{equation}
\Delta f \approx
+ \frac{\partial^2f}{\partial x^2}(\Delta x)^2
+ 2\frac{\partial^2f}{\partial x\partial y}\Delta x\,\Delta y
+ \frac{\partial^2f}{\partial y^2}(\Delta y)^2\tag{10.2.4}
\end{equation}
So we need to understand the shape of a quadratic function of the form
\begin{equation}
h(x,y) = A x^2 + 2B xy + C y^2\tag{10.2.5}
\end{equation}
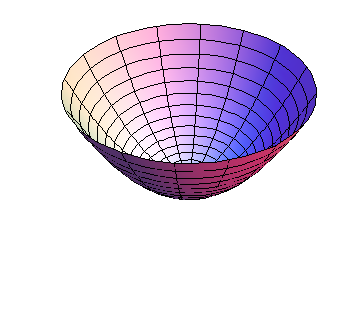
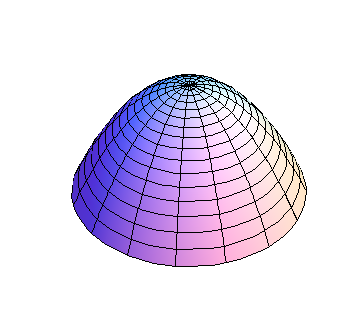
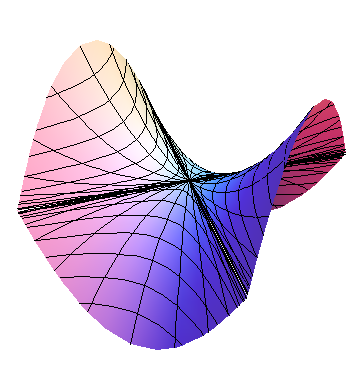
Consider first the simpler case when \(B=0\text{.}\) Then \(h\) is parabolic along both the \(x\) and \(y\) axes; the only question is whether the parabolas open up or down. If \(AC>0\text{,}\) both parabolas open in the same direction, and the graph is a paraboloid, as shown in Figures 10.2.2 and Figure 10.2.1, whereas if \(AC\lt 0\text{,}\) the graph is saddle-shaped, as shown in Figure 10.2.3.
For the general case, we need some algebra. Assume \(C\ne0\) and complete the square, yielding
\begin{align*}
A x^2 \amp+ 2B\,x\,y + C y^2\\
\amp=
C \left(y+\frac{B}{C}x\right)^2 + \left( A - \frac{B^2}{C} \right) x^2\\
\amp= C \left[\left(
y+\frac{B}{C}x\right)^2
+ \left( \frac{AC-B^2}{C^2} \right) x^2 \right]
\end{align*}
and set \(D=AC-B^2\text{.}\) Then if \(D>0\text{,}\) the term in square brackets is positive, and the graph of h is a paraboloid, which opens up if \(C>0\) (a min), and down if \(C\lt 0\) (a max), as shown in Figures 10.2.2 and Figure 10.2.1, respectively. If \(D\lt 0\text{,}\) then the term in square brackets is positive when \(x=0\text{,}\) but negative when \(y=-\frac{B}{C}x\text{;}\) this is a saddle, as shown in Figure 10.2.3. If \(C=0\) but \(A\ne0\text{,}\) a similar argument can be made replacing \(C\) by \(A\text{.}\) If \(A=0=C\) but \(B\ne0\text{,}\) then \(h=xy\text{,}\) which is easily seen to be a saddle. But if all of \(A\text{,}\) \(B\text{,}\) and \(C\) vanish, anything can happen; we need more information. Since \(D=0\) in this latter case, anything can happen if \(D=0\text{.}\)
Combining this argument with the form of \(\Delta f\) given in (10.2.4), we have
\begin{equation}
A = \frac{\partial^2 f}{\partial x^2}
\qquad
B = \frac{\partial^2 f}{\partial x\partial y}
\qquad
C = \frac{\partial^2 f}{\partial y^2}\tag{10.2.6}
\end{equation}
and the argument given here reproduces the second derivative rule given in Section 10.1
